Section 2.6- Rational Functions and Asymptotes

Hello Everybody! This post is on rational functions and their asymptotes.

First, let's take a look at what a rational function looks like:


A rational function is the quotient of two polynomials, N(x) / D(x).

Finding the Domain:

The domain of a rational function of x includes all real numbers except the x values that make the denominator zero.

When faced with a rational function, find the value of x that makes the denominator zero.  Your answer will be the value or values not included in the domain of the function. 

Finding Vertical Asymptotes:

Let's use the same function as before:



When the value of x makes N(x), the numerator, zero, it is an x-intercept of the function.  That value is where the function crosses the x axis on the graph.

When the value of x makes D(x), the denominator, zero, the function becomes undefined.  This x value is not part of the function f(x).

          The line x = a is a vertical asymptote of the graph of f if f(x) or     f(x) as xa

Here's an example:



The domain of this function is all real numbers except -1, because -1 makes the denominator zero, and the function becomes undefined.

 
 As shown in the graph, the function does not touch the vertical line where  x=-1.  Therefore, there is a vertical asymptote at x=-1.  To find the vertical asymptotes, you must find the zeros of the denominator.  These x values are the vertical asymptotes.

Finding Horizontal Asymptotes:

The function above also has a horizontal asymptote.  A horizontal asymptote

is a line y = b on the graph of f  if  f(x) b as x  or x  ...

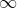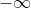 That means that as the value x gets closer to  and , the function approaches the line b, or the horizontal asymptote.  

To find a horizontal asymptote, look first at the degree of the polynomials in the function, then at the leading coefficients of the numerator and denominator...

Consider this function:

Since the degree of the denominator polynomial is bigger than the polynomial in the numerator, the line y=0 is a horizontal asymptote.  Whenever the degree is bigger in the denominator, the horizontal asymptote is the line y=0.

When both polynomials in the numerator and denominatore have the same degree, the horizontal asymptote is given by the ratio of the leading coefficients of both polynomials:

    The ratio of the leading coefficients is 2/3, which is the horizontal asymptote: y=2/3.

Furthermore, when the numerator's degree is greater than the denominator's degree, there is no horizontal asymptote!

 
Holes

Lastly, let's touch upon the concept of holes in the graph of a rational function... 

Let's go back to the function:

 If N(x) = D(x) = 0, then the function f(x) is indeterminate. The graph will have a hole at the point (x, f(x)). 

That's all, folks!

-Henry