Hello all!
Over the chapters and through the tests, to Chapter Three we go...
To start out, let's be like Mr. Wilhelm and slip in some definitions. What are
exponential and
logarithmic functions? They are otherwise known as
transcendental functions; they can't be expressed in terms of algebra.
An
Exponential Function is denoted by;
=a^x "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
BUT:
0<a
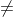
1 and x is any real number.
Graphing
For example purposes, the two functions we'll use are
=2^x "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
and
=4^x "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
Note that as the base number gets larger, the graph increases more rapidly. (Sorry about the scale for the y-axis being different.)
So let's go over the basics for this find of function;
-Domain:
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
-Range:
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
-Intercept:
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
-Increases
-The x-axis is the horizontal asymptote
-Continuous
But what happens if you do something crazy, like put -x as the exponent? Well, what a great question you have...
Let's use the same equations but make -x the exponent.
=2^{-x} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
and
=4^{-x} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
Woah! The graph goes the OPPOSITE way! Crazy! But the same general idea holds true; the larger the base, the more rapidly the graph decreases.
Just like regular algebra, a function with a negative exponent can be written as a fraction instead. For example;
can also be written as
=\frac{1}{2}^{x} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
The basics for this kind of function are...
-Domain:
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
-Range:
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
-Intercept:
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
-Decreasing
-The x-axis is the horizontal aymptote
-Continuous
What to do next...hmm...transforming the parent function sounds fun!
So many possibilities, let's go alphabetically.
When you change a, the graph has a vertical stretch(or compress depending on whether 1>a or a>1).
Changing b horizontally stretches/compresses the graph(unless you make it negative, in which case it flips over the x-axis).
If you were to change c, it would horizontally shift the graph left/right.
Lastly, the changing of d would result in a vertical shift of the graph.
Natural Base
We can't forget about our friend, e. This little guy is known as the
natural base, and it's function is
=e^{x} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
. This e is in fact an irrational number that is approximated to 2.71828... but luckily, your calculator should have this as a key so you don't have to type all of the number in. Just be sure you realize that e isn't a variable, e has value just like 1 and 2, just not as exact.You plug e into your calculator just like any other number.
As far as graphing functions of e, all of the ideas we already went over apply. Just instead of using a constant, put e in as the base. Everything else is the exact same.
Compound Interest
This is fairly straightforward, as long as you know what the formulas and variables are. For n compoundings per year, the equation is
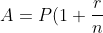^{nt} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
-A stands for balance in an account
-P is principal
-r means annual interest rate(expressed as a decimal)
-n is the number of compoundings per year
-t stands for the amount of time in years
For continuous compounding, the equation is
.
The variables are all the same as in the previous formula, just don't forget that e is an actual number, NOT a variable.
I'm pretty sure that covers the section. If my post doesn't answer all of your questions, ask a buddy, be a book-licker or ask the all knowing, Mr.Wilhelm.
.gif)
.gif)
.gif)
.gif)
.gif)
, then.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)